Mistakes Are Good, Because They Mean You're Learning

I’m going to share something with you about why my students tend to be successful.

Imagine the following thought exercise. You put a math problem in front of a kid, and don’t tell them how to solve it. The math problem isn’t a “familiar” one, so they can’t use formulas. It probably looks a little bit like this:

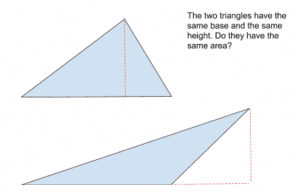
No cheating! They have to argue for a certain answer on the basis of actual reasoning. (For instance, maybe they can come up with a way of dissecting one shape, or both, so that they can be shown to occupy the same amount of space on the page? Or maybe not!)

This type of exercise is almost never done in school, and when it is done, it’s done as an oh-yeah-and-there’s-also-this addendum to the usual laundry list of formulas and pre-solved problems. The usual solution (and something that is often useful) is to provide something along the lines of “incremental feedback” to help the student to discover a preconceived answer. A lot of the time, this is basically harmless. But I think that we are applying this principle much too broadly, and that we’re harming our students as a result.

One of my favorite rogue mathematicians (yes, that’s a thing) is Paul Lockhart. In his brilliant essay “A Mathematician’s Lament” he details what we are depriving our children of when we give them problems and answers at the same time, forbidding them from finding their own answers. Real life, and real human growth, involves stumbling around, not knowing what you’re doing, and finding answers to problems that are intuitive and that work for you. Another modern genius mathematician is Andrew Wiles. It was he who proved Fermat’s Last Theorem, the problem centuries of mathematicians had spent their entire lives trying to crack. He describes the learning process like this:

“Perhaps I can best describe my experience of doing mathematics in terms of a journey through a dark unexplored mansion. You enter the first room of the mansion and it’s completely dark. You stumble around bumping into the furniture, but gradually you learn where each piece of furniture is. Finally, after six months or so, you find the light switch, you turn it on, and suddenly it’s all illuminated.”

We tend not to give students the chance to fumble around in the dark. They are generally not allowed to discover what it is like to prod their way through uncharted intellectual territory; to recognize the steps necessary to solve an unfamiliar type of problem; to know the great joy of discovering an answer that is entirely their own. Instead of the dark mansion Wiles describes, we instead insist on students experiencing math—and, increasingly, other subjects—as a well-lit and guided tour of a staged property. We will show them what to do, and if they get it wrong, then they will be punished, and told the right way to do it. And anyway, we don’t have time to meander through these weird problems and let you waste a bunch of time making mistakes! We have tests to get you ready for!

I want to advance a radical idea: mistakes are not just unpleasantly “normal,” in the sense of scraped knees or pimples. They are good. It is good to face frustration, to be forced to confront unfamiliar problems with minimal assistance. I relentlessly ask my students why something is true, instead of being content with the simple answer “that” it is true. If we are doing a physics problem and kinetic energy has become gravitational potential energy, I will lob them a question about why this has happened. The question of “why” is the most potent one in academics, for if a student can answer the question of “why”—and answer it themselves, from their own storehouse of knowledge—then they have truly mastered something. They have made it their own. This is not possible without mandating that students confront difficult intellectual situations.

This requires enormous restraint on the part of parents and teachers. When we see our children struggling, the most natural thing is to reach in and prevent the struggle. One of the things that gives me the most joy about working with a student, however, is to encourage them to embrace the struggle, to confront intellectual challenges. To make their own arsenal of “why”s. I have met real geniuses before, and they all have one thing in common: they love to tackle difficult problems, with no guidance. I assert that this capacity is one that can be grown. Allowing kids to make mistakes is a good thing, because it means they are learning something that they can learn nowhere else.

When children work with me, I do demand that they understand “why” things work. Whether we are reviewing quadratic equations or going over Of Mice and Men, I require that they demonstrate their understanding to me. I am a private tutor, and of course that job involves sometimes giving students assistance with simply finding answers. However, in the long game of education—the one that really matters—I serve my students better when I force them to confront the occasional frustration. They may have to spend more time on it in the meantime, but when they learn something, they have made it truly their own. This time-honored means of learning occupies less time in the end, because future skills are acquired so much more easily when basic ones have been truly internalized.

One of my earliest experiences tutoring someone in advanced math was when I was in college. As a senior math major, I was tasked with tutoring a younger math major in a difficult topic called “Real Analysis.” This is widely considered the first real math class, the first one that only math majors have to take. The entire class more or less hinges on understanding the topic of “epsilon-delta convergence,” the details of which I won’t bore you with here, except that it’s super important and pretty tough to understand. This student worked for hours and hours with me, over many sessions, to understand this concept. This was twelve years ago, and I still remember the “I found the light switch” look in his eyes. That wouldn’t have happened if I just taught him a bunch of formulas. It only came of the fruit of making mistakes, of being frustrated. I love being a part of that process. It’s why I do what I do, and it’s why my students are successful.